Graphs

Within this section, few further explanations will be added to aid in the understanding of Graphs as part of this module.

A visualisation that personally helps me to understand graphs is imagining vertices as physical locations and the edge cost to be the time distance between them(so a form of a map for example).

Most graphs are defined as a slight alteration of the following rules.

A graph is made up of two sets called Vertices and Edges. The Verticies are drawn from some underlying type, and the set may be finite or infinite. Each element of the Edge set is a pair consisting of two elements from the Vertices set. Graphs are often depicted visually, by drawing the elements of the Vertices set as boxes or circles, and drawing the elements of the edge set as lines or arcs between the boxes or circles. There is an arc between v1 and v2 if (v1,v2) is an element of the Edge set. Adjacency. If (u,v) is in the edge set we say u is adjacent to v (which we sometimes write as u ~ v).

For example the graph drawn below

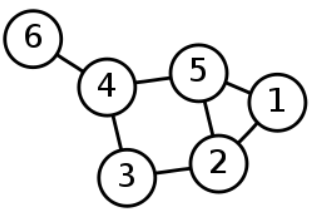
Has the following parts.

The underlying set for the Verticies set is the integers.

The Vertices set = {1,2,3,4,5,6}

The Edge set = {(6,4),(4,5),(4,3),(3,2),(5,2),(2,1),(5,1)}

Graphs can be:

Undirected Graphs : All edges are two way, so A to B with cost 3 means there is also a path from B to A with the same cost.

Directed Graphs : Edges are one way, so A to B with cost 3 does not mean there is a path from B to A.

Unweighted: Traversing through all edges has the same cost, commonly assumed to be 1.

Weighted: There is a cost for traversal for each edge, hence from traversal from A to B the cost of traversal is equal to the weight of that edge and possibly a different weight from B to C.

Common Problems in Graph Theory (Mentioned in the lecture):

Connectivity: If C is reachable from A. Solved by graph traversal algorithms, BFS or DFS.

Shortest Path(and multiple variations): Lowest total cost to C from A. Solved by shortest path algorithms (Djikstra for example). For Unweighted graphs BFS can also be used.

Minimum Spanning Tree: Connect all the vertices with edges with the minimum total weight(edge cost). Solved with Kruskal or Prim Algorithms.

There are a lot of resources available both in the lecture and online for these kind of problems and examples of what can be represented through a graph.